样条曲线
样条曲线(Spline Curve)是一种数学上定义的平滑曲线,通过一组控制点生成,广泛应用于计算机图形学、工程设计、动画制作等领域。以下是关于样条曲线的详细解释:
1. 定义与基本概念
样条曲线是一种分段连续的多项式曲线,通常由多个控制点定义。这些控制点决定了曲线的大致形状,而曲线本身通过插值或逼近的方式生成。样条曲线可以是开放的或闭合的,并且可以由单段或多段构成。
- 插值样条:通过所有控制点生成曲线。
- 逼近样条:不通过所有控制点,而是尽量接近这些点。
样条曲线的数学表达通常采用分段多项式形式,例如三次样条($C^2$连续)或更高阶的样条($C^3$连续)。三次样条是最常用的类型,因为它在控制点之间具有连续的一阶和二阶导数。
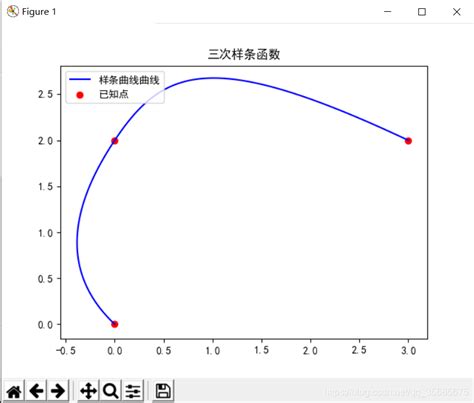
2. 数学描述
样条曲线可以通过以下方式描述:
- 分段多项式:每一段由一个多项式函数表示,例如三次多项式 $ P(x) = a_0 + a_1x + a_2x^2 + a_3x^3 $。
- 边界条件:样条曲线在每个控制点处满足特定的连续性条件,例如一阶导数或二阶导数连续。
对于三次样条,其数学表达式为:
$$ P(x) = \sum_{i=0}^{n} c_i B_i(x) $$
其中,$ B_i(x) $ 是基函数,$ c_i $ 是权重系数。
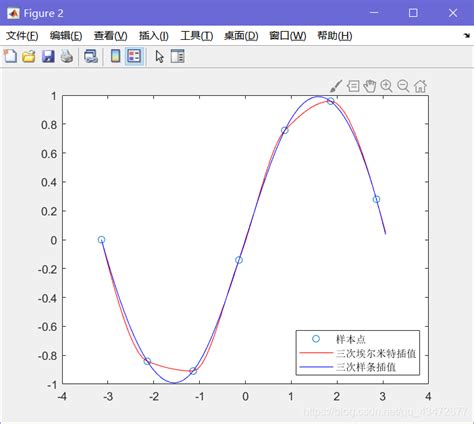
3. 应用领域
样条曲线在多个领域有广泛应用:
- 计算机图形学:用于设计曲线和曲面形状,例如动画路径规划、物体形状设计等。
- 工程设计:用于绘制复杂曲线,如船舶、汽车和飞机的设计。
- 数据拟合:通过样条曲线拟合数据点,生成平滑的曲线。
- 动画制作:用于定义角色或物体的运动轨迹。

4. 常见类型
样条曲线有多种类型,每种类型适用于不同的场景:
- 三次样条:最常用,具有$C^2$连续性。
- B样条:通过控制点生成曲线,具有局部控制特性。
- NURBS(非均匀有理B样条) :用于描述复杂的曲面和曲线,如圆锥曲线。
- 贝塞尔曲线:通过控制点生成平滑曲线,适用于简单的曲线设计。
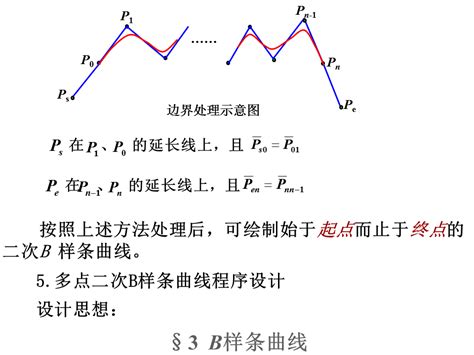
5. 特点与优势
样条曲线具有以下特点:
- 平滑性:通过控制点生成的曲线具有连续的导数,避免了尖锐拐点。
- 灵活性:可以通过调整控制点的位置改变曲线形状。
- 局部控制:修改某一个控制点只会影响曲线的局部区域。
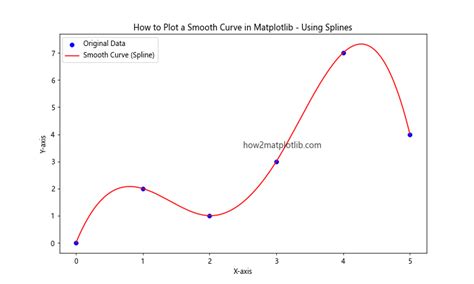
6. 实际应用案例
- CAD软件:如AutoCAD中使用样条曲线绘制复杂曲线。
- 动画制作:通过调整控制点生成平滑的运动轨迹。
- 数据拟合:使用样条曲线拟合实验数据,生成平滑的趋势线。

7. 总结
样条曲线是一种强大的数学工具,通过控制点生成平滑的曲线。它在计算机图形学、工程设计和数据拟合等领域具有广泛的应用。无论是插值样条还是逼近样条,样条曲线都能提供灵活且高效的解决方案。
作者的情感表达细腻入微,让人在阅读中找到了心灵的慰藉。
理论深度可再挖掘,以提升文章厚重感。
?未来展望类?
立意高远,以小见大,引发读者对社会/人性的深层共鸣。